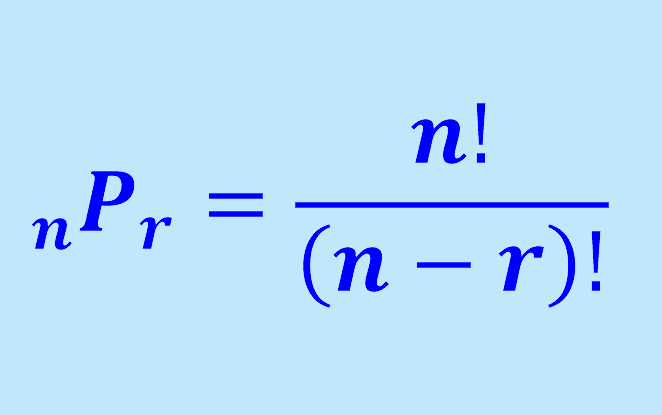

With permutations, we can count the number of different ways of choosing objects from a set if the order of the objects does matter. This is different from combinations, where the order of the objects does not matter.
Here, we will start with a summary of permutations and look at their formula. Then, we will see several examples with answers to understand the application of the permutations formula.
Relevant for…
Learning about permutations with solved examples.
Contents
Relevant for…
Learning about permutations with solved examples.
A permutation is a list of objects, in which the order is important. Permutations are used when we are counting without replacing objects and order does matter. If the order doesn’t matter, we use combinations. In general P(n, k) means the number of permutations of n objects from which we take k objects. Alternatively, the permutations formula is expressed as follows:
| $latex __>=\frac> <<( |
To solve permutations problems, we have to remember that the factorial (denoted as “!”) is equal to the product of all positive integers less than or equal to the number preceding the factorial. For example, $latex 4!=1 \times 2 \times 3 \times 4 = 24$.
In the following examples, we will see the application of the permutations formula. Each example has its respective detailed solution, which can be used to understand the reasoning in the answer to each exercise.
Find the result of the permutation $latex _P_$.